问题
填空题
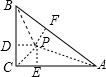
△ABC是直角三角形,两直角边BC=7,AC=24,在△ABC内有一点P,点P到各边的距离都相等,则这个距离为______.
答案
由勾股定理得:AB=
=25,72+242
∵在△ABC内有一点P,点P到各边的距离都相等,
∴P为△ABC的内切圆的圆心,设切点为D、E、F,连接PD、PE、PF、PA、PC、PB,内切圆的半径为R,
则由三角形面积公式得:
×AC×BC=1 2
×AC×R+1 2
×BC×R+1 2
×AB×R,1 2
∴7×24=7R+24R+25R,
R=3,
故答案为:3.
