问题
解答题
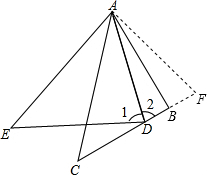
如图,在△ABC中,∠ABC=90°,D为BC上一点,在△ADE中,∠E=∠C,∠1=90°-
(1)∠1=∠2; (2)ED=BC+BD. 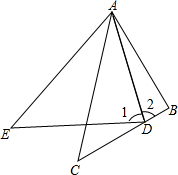 |
答案
证明:(1)由三角形的外角性质,∠BAD+∠ABD=∠1+∠EDC,
∵∠1=90°-
∠EDC,1 2
∴∠BAD+90°=90°-
∠EDC,1 2
∴∠BAD=
∠EDC,1 2
延长DB至F,使BF=BD,
则AB垂直平分DF,
∴∠BAD=
∠DAF,AD=AF,1 2
∴∠DAF=∠EDC,∠2=∠F,
在△ADF中,∠F+∠DAF=∠1+∠EDC,
∴∠1=∠F,
∴∠1=∠2;
(2)在△AED和△ACF中,
,∠1=∠F ED=CF ∠E=∠C
∴△AED≌△ACF(ASA),
∴ED=CF,
∵CF=BC+BF=BC+DB,
∴ED=BC+BD.