问题
问答题
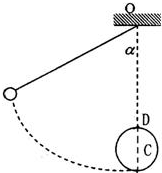
长为L的轻绳一端系一小球,另一端悬于O点.小球从与竖直方向成a角处释放,到最低点与一钉子C相碰后绕C做圆周运动,若半径CD=
L,欲使小球刚好能通过最高点,则1 5
(1)a角应为多大?
(2)若小球释放位置不变,则到达最低点时碰钉子后瞬间绳子对小球的拉力等于多大?
答案
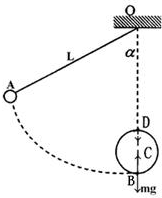
1)从A→D过程中,
mgL(1-cosα)-mg2R=
mVD21 2
在D处,由于小球刚好能通过最高点,则有
mg=mv 2D R
由题意得R=L 5
联立解得α=60°
α角应为60°.
(2)从A到B,由机械能守恒有
mgL(1-cos60°)=
mvB21 2
在B处受力如图,由牛顿第二定律
T-mg=mv 2B R
R=L 5
联立解得T=6mg;
到达最低点时碰钉子后瞬间绳子对小球的拉力等于6mg.
