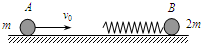
如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离.(弹簧始终处于弹性限度以内)
(1)在上述过程中,弹簧的最大弹性势能是多大;
(2)若开始时在B球的右侧某位置固定一块挡板(图中未画出),在A 球与弹簧分离之前使B球与挡板发生碰撞,并在碰后立刻将挡板撤走.设B球与固定挡板的碰撞时间极短,碰后B球的速度大小不变但方向相反.试求出此后弹簧的弹性势能最大值的范围.
(1)当A球与弹簧接触以后,在弹力作用下减速运动,而B球在弹力作用下加速运动,弹簧势能增加,当A、B速度相同时,弹簧的势能最大.
设A、B的共同速度为v,弹簧的最大势能为E,则A、B系统动量守恒:mv0=(m+2m)v①
由机械能守恒:m=(m+2m)v2+E…②
联立两式得:E=m…③
(2)设B球与挡板碰撞前瞬间的速度为vB,此时A的速度为vA.
系统动量守恒:mv0=mvA+2mvB…④
B与挡板碰后,以vB向左运动,压缩弹簧,当A、B速度相同(设为v共)时,弹簧势能最大,为Em,则:mvA-2mvB=3mv共…⑤
m=×3m+Em…⑥
由④⑤两式得:v共=代入⑥式,化简得:Em=[-(vB-)2+]…⑦
而当弹簧恢复原长时相碰,vB有最大值vBm,则:
mv0=mvA′+2mvBm mv02=mvA′2+×2mvBm2
联立以上两式得:vBm=v0即vB的取值范围为:0<≤v0…⑧
结合⑦式可得:当vB=时,Em有最大值为:m…⑨
当vB=时,Em有最小值为:m
答:(1)弹簧的最大弹性势能是E=m.
(2)此后弹簧的弹性势能最大值的范围为[m,m].