问题
问答题
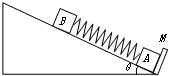
如图,一倾角为30°的光滑斜面,底端有一与斜面垂直的固定档板M,物块A、B之间用一与斜面平行轻质弹簧连结,现用力缓慢沿斜面向下推动物块B,当弹簧具有5J弹性势能时撤去推力,释放物块B;已知A、B质量分别为5kg、2kg,弹簧的弹性势能表达式为EP=
kx2,其中k为弹簧的劲度系数,大小为1000N/m,x为弹簧形变量.(g取10m/s2)1 2
(1)求当弹簧恢复原长时,物块B的速度;
(2)试判断在B上升过程中,能否将A 拉离档板?若能,请计算A刚离开档板时B的动能;若不能,请计算B在最高点处的加速度.
答案
(1)由EP=
kx2得,刚撤去推力时,弹簧的压缩量x1=0.1m…①1 2
弹簧恢复原长的过程中,物块B和弹簧组成的系统机械能守恒,
由EP=mBgx1sinθ+
mBv2…②得1 2
v=2m/s…③
(2)假设A能被拉离挡板,在A刚被拉离时,有弹簧弹力F=mAgsinθ…④
结合F=kx2,此时弹簧伸长量x2=0.025m…⑤
此时弹性势能EP=0.3125J…⑥
相对于弹簧原长处重力势能增量为△EP=mBg△h=0.25J…⑦
因为弹簧处于原长时物块B的动能Ek0=
mBv2=4J…⑧1 2
由于Ek0>EP+△EP,所以能将物块A 拉离档板,且此时物块B的动能为:Ekt=Ek0-EP-△EP,得Ekt=3.44J…⑨
答:
(1)当弹簧恢复原长时,物块B的速度为2m/s;
(2)在B上升过程中,能将物块A拉离档板,且此时物块B的动能为3.44J.
