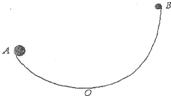
（1）设A、B在O点的速度大小分别为v_A、v_B．

由机械能守恒定律得：Mgh=

解得，v_A=

设碰撞n次后大物体的速度最小，最小速度为零，则根据动量守恒得：

  Mv_A-nmv_B=（M+m）v

当v=0时，Mv_A-nmv_B=0，则得n=50次

（2）当大物体的速度达到v_A时，恰好能越过A点．

 第一次碰撞：Mv_A-mv_B=（M+m）v

 设再碰撞k次：（M+m）v+kmv_B=（M+m+km）v_A，

联立解得 k=3

故共碰4次．

（3）第1次碰撞：Mv_A-mv_B=（M+m）v₁，

    第2次碰撞：（M+m）v₁+mv_B=（M+2m）v₂，

    第3次碰撞：（M+m）v₂-mv_B=（M+3m）v₃，

    第4次碰撞：（M+m）v₃+mv_B=（M+4m）v₄，

   …

第50次碰撞：（M+49m）v₄₉+mv_B=（M+50m）v₅₀，

联立解得，v₅₀=

根据机械能守恒得：Mgh′=

解得h′=

答：

（1）若每当大物体向右运动到O点时，都有一个小物体与之碰撞，碰撞50次后大物体的速度最小．

（2）若大物体第一次向右运动到0点时，和小物体碰撞，以后每当大物体向左运动到0点时，才与一个小物体碰撞，共碰撞4次后大物体能越过A点．

（3）若每当大物体运动到0点时，都有一个小物体与之碰撞，碰撞50次后，大物体运动的最大高度为h的