如图所示,质量为M=20kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L=5m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问:
(1)碰撞前瞬间两车的速度大小各为多少?
(2)若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少多大?
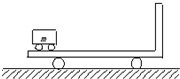
(1)如图,电动车向右运动的过程中长板车将向左运动,在运动过程中满足动量守恒
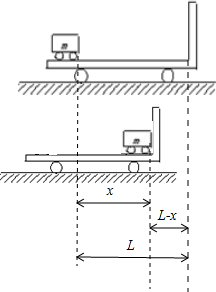
由图可知,令电动车相对地面产生的位移大小为x,则长木板车的位移大小为(L-x),负号表示长木板车的位移方向与电动车位移方向相反,令与挡板相碰前电动车的速度为vm,长木板车的速度vM,则据动量守恒有:
mvm+MvM=0…①
又因为在碰撞前两车均做初速度为0的匀加速运动,所以有:
=. vm
,电动车运动的时间t=vm 2
=x . vm
=2s…②2x vm
=. vM
,长木板车运动的时间t=vM 2
=L-x . vM
=2s…③2(L-x) vM
由①②③式可解得:
vm=4m/s
vM=1m/s
(2)因为在碰撞过程中无机械能损失,又因为在碰撞中系统动量守恒可知碰撞前后,两车速度均反向,且不改变原速度的大小
vm′=4m/s,方向向左;
vM′=1m/s,方向向右.
∵MvM=mvm
∴系统总动量为0,即当系统稳定时两车均静.
因为克服摩擦力做的功应该等于系统损失的机械能,要使电动车不滑离长木板车,则长木板车的长度满足:
μmgL≥
mvm′2+1 2
MvM′21 2
代入数据可解得:μ≥0.2
答:(1)碰撞前瞬间两车的速度大小分别为vm=4m/s,vM=1m/s
(2)若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少为0.2.

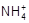 +OH-= NH3↑+H2O
+OH-= NH3↑+H2O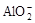 +H2
+H2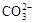 +H2O
+H2O