问题
问答题
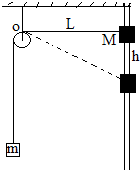
如图,光滑竖直杆上套有质量为M=0.7kg的滑块,通过轻质细绳跨过光滑滑轮与质量为m=0.5kg的物块相连.滑轮上边缘到竖直杆的距离L=4m,开始时细绳右半部分保持水平.由静止释放滑块M,当M沿杆下滑h=3m时,滑块M下滑的速度是多少?(设细绳足够长,不计空气阻力.g=10m/s2.)
答案
设M下落的速度为v,此时绳子与水平方向夹角θ,则物块m上升的速度
=vsinθ,又sinθ=v ′
=h
+(L(h ) 2 ) 2
,所以m上升的速度为3 5
=v ′
v;3 5
M下落h=3m,则m上升高度为h′=
-L=1m(L
+(h) 2 ) 2
由系统机械能守恒:有Mgh=mgh′+
M1 2
+v 2
m1 2
,代入数据解得v=v ′2
m/s=6.03m/s.20 11 11
即滑块M下滑的速度是6.03m/s.
