问题
问答题
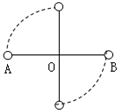
如图所示,有一根轻杆AB,可绕O点在竖直平 面内自由转动,在AB两端分别固定有质量为m和2m的小球,OA和OB的长度相等,都等于a.开始时,AB静止在水平位置,释放后,AB杆转到竖直位置时,求:
(1)A、B两端小球总的重力势能减少多少?
(2)A、B两端小球的速度大小各是多少?
(3)如果杆从水平位置转至竖直位置时A球对杆的压力恰好为零,那么A、B两球的质量之比是多少?
答案
(1)以水平位置为零势能面,则初位置的重力势能为零,末位置的重力势能为:EP=EPA+EPB=mga-2mga=-mga
所以A、B两端小球总的重力势能减少mga
(2)AB的角速度相等,根据v=ωr可知AB的线速度也相等,根据机械能守恒定律得:
-△EP=△EK
×3mv2=mga1 2
解得:
vA=vB=2ga 3
(3)对A进行受力分析,根据向心力公式得:
mAg=mAvA2 a
解得:vA=ga
根据机械能守恒定律得:
(mA+mB)vA2=mAga-mBga1 2
解得:
=mA mB 1 3
答:(1)A、B两端小球总的重力势能减少mga,
(2)A、B两端小球的速度大小都为2ga 3
(3)如果杆从水平位置转至竖直位置时A球对杆的压力恰好为零,那么A、B两球的质量之比是1:3.
