如图甲所示,小车B静止在光滑水平上,一个质量为m的铁块A(可视为质点),以水平速度v0=4.0m/s滑上小车B的左端,然后与小车右挡板碰撞,最后恰好滑到小车的中点,已知
=3,小车车面长L=1m.设A与挡板碰撞无机械能损失,碰撞时间可忽略不计,g取10m/s2,求:M m
(1)A、B最后速度的大小;
(2)铁块A与小车B之间的动摩擦因数;
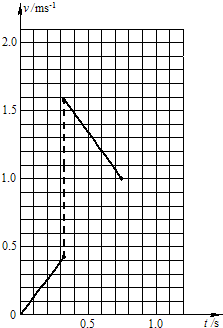
(3)铁块A与小车B的挡板相碰撞前后小车B的速度,并在图乙坐标中画出A、B相对滑动过程中小车B相对地面的速度v-t图线.

(1)对A、B系统,由动量守恒定律得:
Mv0=(M+m)v,解得v=
=1m/s;mv0 M+m
(2)A、B系统整个过程,由动能定理得:
μmg×1.5L=
m1 2
-v 20
(M+m)1 2
,v 2
解得:μ=
=0.4;v02-4v2 4gL
(3)设A、B碰撞前速度分别为v10和v20,
对系统动量守恒 mv0=mv1+Mv2,
对系统能量转化和守恒定律得:
μmgL=
mv02-1 2
mv102-1 2
M1 2 v 220
带入数据联立方程,解得v10=1+
=2.732 m/s,(舍v10=1-3
=-0.732m/s)3
v20=1-
=0.423m/s,3 3
该过程小车B做匀加速运动,
由牛顿第二定律得:μmg=MaM,
解得:aM=
m/s2,v20=aMt1,t1=0.317s,4 3
A、B相碰,设A、B碰后A的速度为v1和 v2
A、B系统动量守恒:mv0=mv1+Mv2
对系统机械能守恒
mv102+1 2
M1 2
=v 220
mv12+1 2
M1 2
,v 22
带入数据联立方程,解得v1=1-
=-0.732 m/s,(舍v1=1+3
m/s)3
“-”说明方向向左;v2=1+
=1.577m/s,3 3
该过程小车B做匀减速运动,-μmg=MaM,解得aM=-
m/s2,4 3
到最终相对静止:v=v2+aMt2,t2=0.433s,
所以,运动的总时间为:t=t1+t2=0.75s,
小车B的v-t图如图所示;
答:(1)A、B最后速度的为1m/s;
(2)铁块A与小车B之间的动摩擦因数为0.4;
(3)小车B相对地面的速度v-t图线如图所示.
