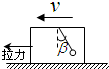
水平地面上放置一个质量为M的木箱,箱中的顶端用一长为L的轻细绳悬挂着一质量为m的小铁球,地面与箱子的动摩擦因数为μ.对木箱施加一个水平向左的恒定拉力,系统稳定后轻细绳向右偏离竖直方向β角,某时木箱的速度方向向左,大小为v,如图所示.
(1)求此时水平拉力的大小.
(2)此时,由于某种原因木箱突然停下来且以后保持静止不动,求以后运动过程中小球对细绳的最大拉力.(整个运动过程中,小球与木箱不碰撞)
(1)以木箱和小球整体为研究对象,根据牛顿第二定律有:
F-μ(M+m)g=(M+m)a ①
以小球为研究对象,受力分析,根据牛顿定律有:
a=gtanβ ②
根据方程①②解得:
F=μ(M+m)g+μ(M+m)gtanβ
(2)小球摆到最低点的过程中,根据机械能守恒定律有:
mv2+mgL(1-cosβ)=1 2
mvr2 ③1 2
在最低点细绳的拉力最大,对小球受力分析,根据牛顿第二定律有:
T-mg=m
④v 2r L
根据方程③④解得:细绳的最大拉力为:T=3mg-2mgcosβ+mv2 L
根据牛顿第三定律可知:小球对细绳的最大拉力为:
T=3mg-2mgcosβ+mv2 L
答:(1)水平拉力为μ(M+m)g+μ(M+m)gtanβ;(2)小球对细绳的最大拉力为3mg-2mgcosβ+m
.v2 L
