问题
问答题
设b>a>0,证明:
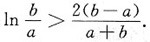
答案
参考答案:
[分析]:当b>a>0时,[*]
令f(x)=(lnx-lna)(a+x)-2(x-a)(x≥a),
因为[*]
[*]
所以f’(x)“↗”,又f(a)=0,于是f’(x)≥0(x≥a),
因而f(x)“↗”,又f(a)=0,故当b>a>0时,f(b)>f(a)=0,
即(lnb-lna)(a+b)-2(b-a)>0,
亦即[*]
设b>a>0,证明:
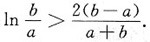
参考答案:
[分析]:当b>a>0时,[*]
令f(x)=(lnx-lna)(a+x)-2(x-a)(x≥a),
因为[*]
[*]
所以f’(x)“↗”,又f(a)=0,于是f’(x)≥0(x≥a),
因而f(x)“↗”,又f(a)=0,故当b>a>0时,f(b)>f(a)=0,
即(lnb-lna)(a+b)-2(b-a)>0,
亦即[*]