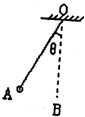
如图所示,质量为m的小球用长度为L的轻质细绳悬挂于O点,现将它拉至A处,使细绳与竖直方向的夹角为θ(θ<5°),然后无初速释放,不计空气阻力作用,它经过一段时间第一次到达最低点B.
求:(1)所经历的时间t
(2)该过程中重力产生的冲量大小IG
(3)该过程中小球的动量变化△P
(4)该过程中绳的拉力产生的冲量大小IF.
(1)由单摆的周期公式可得:
T=2π
--------------------------------①L g
由A第一次到B,小球所用时间是四分之一周期,即:t=
T=1 4 π 2
------②L g
(2)由于重力是恒力,由冲量定义可知重力的冲量为:IG=mgt=
πm1 2
----------------③Lg
(3)动量的变化等于末动量减去初动量:△P=PB-PA------------------------------④
又PA=0--------------------------------⑤
PB=mvB---------------------------------⑥
从A到B的过程中,由机械能守恒定律得:
m1 2
=mgL(1-cosθ)--------------⑦v 2B
由④⑤⑥⑦,可解得:△P=m
------------------⑧2gL(1-cosθ)
(1)从A到B的过程中,小球在重力和绳的拉力的冲量作用下,动量的改变量为△P,且方向水平,又因重力的冲量方向向下,所以由矢量的合成法则得:
IF2=△P2+IG2----------------------------⑨
由③⑧⑨式得:IF=m
.2gL(1-cosθ)+
gLπ2 4
答:(1)所经历的时间t为π 2
.L g
(2)该过程中重力产生的冲量大小IG为
πm1 2
.Lg
(3)该过程中小球的动量变化△P为m
.2gL(1-cosθ)
(4)该过程中绳的拉力产生的冲量大小IF为m
.2gL(1-cosθ)+
gLπ2 4
