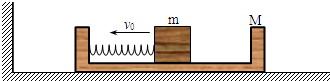
如下图所示,轻质弹簧将质量为m的小物块连接在质量为M(M=3m)的光滑框架内.小物块位于框架中心位置时弹簧处于自由长度.现设框架与小物块以共同速度v0沿光滑水平面向左匀速滑动.
(1)若框架与墙壁发生碰撞后速度为零,但与墙壁不粘连,求框架脱离墙壁后的运动过程中,弹簧弹性势能的最大值.
(2)若框架与墙壁发生碰撞以一定速度反弹,在以后过程中弹簧的最大弹性势能为mvo2,求框架与墙壁碰撞时损失的机械能△E1.
(3)在(2)情形下试判定框架与墙壁能否发生第二次碰撞?若不能,说明理由.若能,试求出第二次碰撞时损失的机械能△E2.(设框架与墙壁每次碰撞前后速度大小之比不变)
(1)框架与墙壁碰撞后,物块以V0压缩弹簧,后又返回,
当返回原位时框架开始离开,由机械能守恒知,此时物块速度是v0方向向右.
设弹簧有最大势能时共同速度为v,由动量守恒定律知:mv0=4mv,
由能量守恒定律mv02=×4mv2+EPx,
解得:EPX=mv02;
(2)设框架反弹速度为v1,最大势能时共同速度为v,则
由动量、能量守恒定律得
3mv1-mv0=4mv,
×3mv12+mv02=×4mv′2+mv02,
解得:v1=,v1′=-v0(舍去),
代入解得:v′=0,
△E1=×3mv02-×3mv12=mv02,
(3)由(2)知第一次碰后反弹后,二者总动量为零,故当弹簧再次伸展后仍可继续与墙壁相撞,并以V1=速度与墙壁相撞,由题意知,
=,所以v2=,
故△E2=×3m()2-×3m()2=mv02,
答:(1)弹簧弹性势能的最大值为mv02;
(3)框架与墙壁碰撞时损失的机械能为mv02;
(4)能,第二次碰撞时损失的机械能为mv02.