问题
问答题
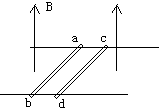
图中两根足够长的平行光滑导轨,相距1m水平放置,磁感应强度B=0.4T的匀强磁场竖直向上穿过整个导轨所在的空间.金属棒ab、cd质量分别为0.1kg和0.2kg,电阻分别为0.4Ω和0.2Ω,并排垂直横跨在导轨上.若两棒以相同的初速度3m/s向相反方向分开,不计导轨电阻,求:
(1)金属棒运动达到稳定后的ab棒的速度大小;
(2)金属棒运动达到稳定的过程中,回路上释放出的焦耳热;
(3)金属棒运动达到稳定后,两棒间距离增加多少?
答案
(1)ab、cd棒组成的系统动量守恒,最终具有共同速度V,以水平向右为正方向,
则mcdV0-mabV0=(mcd+mab)V
∴V=1m/s
(2)根据能量转化与守恒定律,产生的焦耳热为:
Q=△ΕΚ减=
(mcd+mab)(V02-V2)=1.2J1 2
(3)对cd棒利用动量定理:
-BIL•△t=mcd(V-V0)
∴BLq=mcd (V0-V)
又 q=
=△φ R1+R2 BL△s R1+R2
∴△s=mcd(V0-V)(R1+R2)•
=1.5 m1 B2L2
答:(1)金属棒运动达到稳定后的ab棒的速度大小是1m/s;
(2)金属棒运动达到稳定的过程中,回路上释放出的焦耳热是1.2J;
(3)金属棒运动达到稳定后,两棒间距离增加1.5 m
