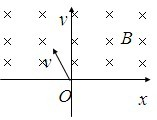
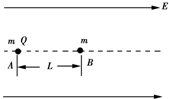
在光滑绝缘的水平台面上,存在平行于水平面向右的匀强电场,电场强度为E.水平台面上放置两个静止的小球A和B(均可看作质点),两小球质量均为m,A球带电荷量为+Q,B球不带电,A、B连线与电场线平行.开始时两球相距L,在电场力作用下,A球开始运动(此时为计时零点,即t=0),后与B球发生对心碰撞,碰撞过程中A、B两球总动能无损失.设在各次碰撞过程中,A、B两球间无电量转移,且不考虑两球碰撞时间及两球间的万有引力.
(1)第一次碰撞结束瞬间A、B两球的速度各为多大?
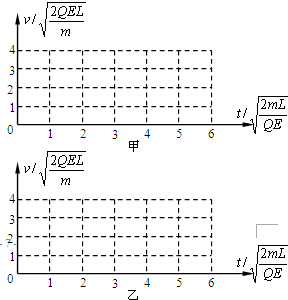
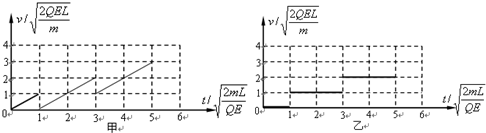
(2)分别在甲、乙坐标系中,用实线作出A、B两球从计时零点到即将发生第三次碰撞这段过程中的v-t图象.要求写出必要的演算推理过程.
(3)从计时零点到即将发生第三次碰撞这段过程中电场力共做了多少功?
(4)若要求A在运动过程中对桌面始终无压力且刚好不离开水平桌面(v=0时刻除外),可以在水平面内加一与电场正交的磁场.请写出磁场B(t)与时间t的函数关系.(不考虑相对论效应)
(1)A球的加速度a=QE m
碰前A的速度vA1=
=2aL
,碰前B的速度vB1=0.2QEL m
A、B碰撞后交换速度,设碰后A、B球速度分别为vA1′、vB1′
vA1′=0 vB1′=vA1=2QEL m
(2)A、B球发生第一次、第二次、第三次的碰撞时刻分别为t1、t2、t3.
则 t1=
=vA1-0 a 2mL QE
第一次碰后,经t2-t1时间A、B两球发生第二次碰撞,设碰前瞬间A、B两球速度分别为vA2和vB2
vB1′(t2-t1)=
a(t2-t1)2 得:t2=3t11 2
vA2=a(t2-t1)=2at1=2vA1=2
vB2=vB1′=2QEL m 2QEL m
第二次碰后瞬间,A、B两球速度分别为vA2′和vB2′,经t3-t2时间A、B两球发生第三次碰撞,并设碰前瞬间A、B两球速度分别为vA3和vB3
则 vA2′=vB2=
vB2′=vA2=22QEL m 2QEL m
当vB2′(t3-t2)=vA2′(t3-t2)+
a(t3-t2)2 发生第三次碰撞,易得t3-t2=t2-t1 1 2
vA3=vA2′+a(t3-t2)=3
vB3=vB2′=22QEL m 2QEL m
(3)由(2)问中所求的物理量,得
W电=(
mvA32+1 2
mvB32)-0=13QEL.1 2
(4)对A球由平衡条件得 BQvA=mg B=
且a=mg QvA
. 解得QE m
从A开始运动到发生第一次碰撞 B(i)=
=mg Qat
0<t≤m2g Q2Et 2mL QE
从第一次碰撞到发生第二次碰撞B(i)=m2g Q2E(t-
)2mL QE
从第二次碰撞到发生第三次碰撞B(i)=
3m2g Q2E(t-2
)2mL QE
≤t≤52mL QE 2mL QE
从第三次碰撞到发生第四次碰撞B(i)=
5m2g Q2E(t-3
)2mL QE
≤t≤72mL QE 2mL QE
以此类推,从第n次碰撞到发生第n+1次碰撞
B(i)=m2g Q2E(t-n
)2mL QE
(2n-1)
≤t≤(2n+1)2mL QE
(n=1,2,3,4…..)2mL QE
答:(1)第一次碰撞结束瞬间A、B两球的速度各为0,
.2QEL m
(2)如图所示.
(3)从计时零点到即将发生第三次碰撞这段过程中电场力共做了13QEL.的功.
(4)磁场B(t)与时间t的函数关系B(i)=
,(2n-1)m2g Q2E(t-n
)2mL QE
≤t≤(2n+1)2mL QE
(n=1,2,3,4…..).2mL QE

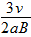 ,正电荷
,正电荷 ,正电荷
,正电荷 ,负电荷
,负电荷 ,负电荷
,负电荷