问题
问答题
如图所示,光滑的半球形固定在水平面上,其半径为R,有一小球(可视为质点)静止在半球形的最高点,小球受一扰动沿球面向下滚动,初速忽略不计,重力加速度为g.
求:(1)小球落到地面时的速度大小.
(2)小球落到地面时速度的水平分量和竖直分量.
答案
(1)小球从开始向下滚动到落地过程,由机械能守恒定律得:
mv2=mgR 1 2
解得:v=2gR
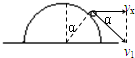
(2)球离开球面时满足:mgcosα=m v 21 R
由机械能守恒定律得:mgR(1-cosα)=
m1 2 v 21
解得:v1=
,cosα=
gR2 3 2 3
离开球面后,小球的水平速度不变.
∴vx=v1cosα=2 3
,vy=
gR2 3
=
-v 2 v 2x
gR46 27
答:
(1)小球落到地面时的速度大小是
.2gR
(2)小球落到地面时速度的水平分量和竖直分量分别为2 3
和
gR2 3
.
gR46 27
