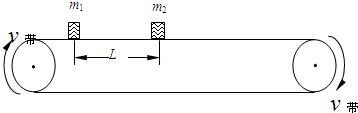
质量为m1=2.0kg的物块随足够长的水平传送带一起匀速运动,传送带速度大小为v带=3.0m/s,方向如图所示,在m1的右侧L=2.5m处将质量为m2=3.0kg的物块,无初速度放上传送带,在m1、m2碰后瞬间m2相对传送带的速度大小为1.0m/s,之后当其中某一物块相对传送带的速度为0时,传送带立即以2.0m/s2的加速度制动,最后停止运动.设两物块与传送带间的动摩擦因数均为0.10,传送带的运动情况不受m1、m2的影响,且m1、m2碰撞时间极短.求:
(1)物体m2刚开始滑动时的加速度;
(2)碰撞后两物块的速度;
(3)两物块间的最大距离.
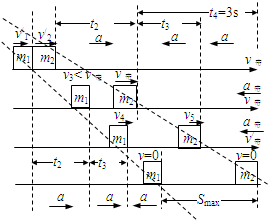
(1)刚开始滑动时,
根据牛顿第二定律得
a=μg=1m/s2 方向向左
(2)设经t1时间m1、m2相碰,有
a1 2
+L=vt1 t 21
t1=1s t′1=5s(由上述分析可知,不合题意,舍去)
碰前m2的速度 v2=at1=1m/s
由题意可知:碰后m2的速度 v′2=2m/s 或 v∥2=4m/s
分别由动量守恒定律得 m1v带+m2v2=m1v′1+m2 v′2与m1v带+m2v2=m1v∥1+m2 v∥2 …1'
得碰后m1的速度 v′1=1.5m/s 或 v∥1=-1.5m/s
检验:由于
m11 2
+v 2
m21 2
<v 21
m11 2
+v′ 21
m21 2 v′ 22
故v∥1=-1.5m/s,v∥2=4m/s 这组数据舍去
∴碰后m1的速度为v′1=1.5m/s向右,m2的速度为v′2=2m/s向右…1'
(3)因碰后两物体均做匀加速运动,加速度都为a=1m/s2,所以m2先达到传送带速度,
设m2达到传送带速度的时间为t2,
有 v带=v′2+at2 t2=1s
此时m1的速度v3=v′1+at2=2.5m/s<v带
故从t2之后m1继续加速,m2和传送带开始减速,
直到m1和传送带达到某个共同速度v4后,
m1所受摩擦力换向,才开始减速运动,
设m1继续加速的时间为t3
则v4=v3+a t3=v带-a带t3 t3=
s1 6
m1的速度为v4=v3+a t3=
m/s 8 3
此时m2的速度为v5=v带-a t3=
m/s,之后m1、m2均做匀减速运动,17 6
因为在整个过程中m2的速度始终大于m1的速度,
所以在m1、m2都静止时两物块位移最大
m2碰后运动的总位移s2=
-v2-v′ 22 2a
=7m0-v2 2×(-a)
m1碰后运动的总位移s1=
-
-v′v 24 21 2a
=6m 0 -v 24 2×(-a)
两物块间最大距离△s=1m.
答:(1)物体m2刚开始滑动时的加速度是1m/s2 方向向左;
(2)碰后m1的速度为v′1=1.5m/s向右,m2的速度为v′2=2m/s向右
(3)两物块间的最大距离是1m.
