如图(a)所示,两根足够长的光滑平行金属导轨相距为l,导轨平面与水平面成θ角,下端通过导线连接的电阻为R.质量为m、阻值为r的金属棒ab放在两导轨上,棒与导轨垂直并始终保持良好接触,整个装置处于垂直导轨平面向上的磁场中.
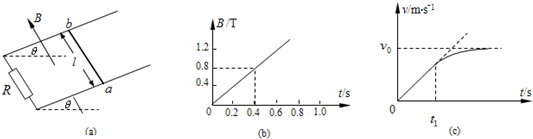
(1)若金属棒距导轨下端距离为d,磁场随时间变化的规律如图(b)所示,为保持金属棒静止,求加在金属棒中央、沿斜面方向的外力随时间变化的关系.
(2)若所加磁场的磁感应强度大小恒为B′,通过额定功率Pm的小电动机对金属棒施加沿斜面向上的牵引力,使其从静止开始沿导轨做匀加速直线运动,经过时间t1电动机达到额定功率,此后电动机功率保持不变.金属棒运动的v-t图象如图(c)所示.求磁感应强度B′的大小.
(3)若金属棒处在某磁感应强度大小恒定的磁场中,运动达到稳定后的速度为v,在D位置(未标出)处突然撤去拉力,经过时间t2棒到达最高点,然后沿轨道返回,在达到D位置前已经做匀速运动,其速度大小为
v,求棒在撤去拉力后所能上升的最大高度.1 5
(1)金属棒沿斜面方向受力平衡,外力应沿斜面向上,设其大小为F1,则
F1-mgsinθ-B1Il=0
由图(b)可知,磁感应强度B的大小与t关系为B1=2t
回路中产生的感应电动势 E=
=△ϕ △t
,S=l•d,△B•S △t
此时回路中的感应电流 I=E R+r
得 F1=mgsinθ+B1
l=mgsinθ+42•l•d R+r
tl2d R+r
(2)由图(c)可知,金属棒运动的最大速度为v0,此时金属棒所受合力为零.
设金属棒此时所受拉力大小为F2,流过棒中的电流为Im,则 F2-mgsinθ-B′Iml=0
Em=B´lv0
Pm=F2•vm
得
-mgsinθ-B′Pm v0
l=0B′lv0 R+r
解得 B′=1 l (
-Pm v 20
)(R+r)mgsinθ v0
(3)设磁感应强度为B,棒沿斜面向上运动时,mgsinθ+BIl=ma得
a=gsinθ+B2l2vt m(R+r)
取极短时间△t,速度微小变化为△v,△v=a△t,△s=v△t
得 △v=gsinθ△t+B2l2v△t m(R+r)
在上升的全过程中,∑△v=gsinθ∑△t+B2l2∑△s m(R+r)
即0-v=-[t2gsinθ+
]B2l2s m(R+r)
又下滑到匀速时有 mgsinθ-
=0B2l2v 5(R+r)
由上两式得s=
-v2 5gsinθ vt2 5
上升的高度H=s•sinθ=v2-vgt2sinθ 5g
答:
(1)加在金属棒中央、沿斜面方向的外力随时间变化的关系是F1=mgsinθ+4
t;l2d R+r
(2)磁感应强度B′的大小为1 l
;(
-Pm v 20
)(R+r)mgsinθ v0
(3)棒在撤去拉力后所能上升的最大高度是
.v2-vgt2sinθ 5g

