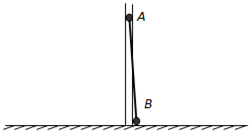
如图所示,A、B两小球用轻杆连接,A球只能沿内壁光滑的竖直滑槽运动,B球处于光滑水平面内.开始时杆竖直,A、B两球静止.由于微小的扰动,B开始沿水平面向右运动.已知A球的质量与B球的质量均为m=1kg,杆长L为=0.2m.
(1)某同学用 mAgL=
mAv2+1 2
mBv2…,求得A球着地时的速度.你认为正确吗?若正确,请接着进行下面的计算;若不正确,请你给出正确的答案.1 2
(2)A球机械能最小时,水平面对B球的支持力为多大?
(3)当A球机械能最小时,杆与竖直方向夹角的余弦值为多大?
(1)不准确,因为A球刚着地时,B球速度为零;
正确解法如下:设此时A球速度为v,由系统机械能守恒得:mAgL=
mAv2,解得v=1 2
=2m/s;2gL
(2)当A球机械能最小时,B球速度最大,此时B球的加速度为零,则杆对球的作用力为零,设小球受到的支持力为N,对B球受力分析可得:
N=mBg=10N;
(3)设满足题干条件时杆与竖直方向的夹角为θ,A、B两球的速度各为vA、vB,系统满足机械能守恒,则:
mAgL(1-cosθ)=
mA1 2
+v 2A
mB1 2 v 2B
且vA和vB沿杆方向分速度大小相等,即vAcosθ=vBsinθ
联立以上两式解得:vB=2gL(1-cosθ)cos2θ
当A球机械能最小时,vB达最大
上式可以写成:
vB=
=2gL(1-cosθ)cos2θ gL(2-2cosθ)cosθ•cosθ
即当cosθ=(2-2cosθ)时,vB最大,亦即此时A球机械能最小,所以cosθ=
.2 3
答:(1)解法不正确,A的速度为2m/s;
(2)A球机械能最小时,水平面对B球的支持力为10N;
(3)当A球机械能最小时,杆与竖直方向夹角的余弦值为
.2 3
