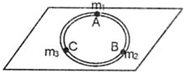
如图所示,一内壁光滑的环形细圆管固定在水平桌面上,环内间距相等的三位置处,分别有静止的大小相同的小球A、B、C,质量分别为m1=m,m2=m3=1.5m,它们的直径略小于管的直径,小球球心到圆环中心的距离为R,现让A以初速度v0沿管顺时针运动,设各球之间的碰撞时间极短,A和B相碰没有机械能损失,B与C相碰后能结合在一起,称为D.求:
(1)A和B第一次相碰后各自的速度大小;
(2)B和C相碰结合在一起后对管沿水平方向的压力大小;
(3)A和B第一次相碰后,到A和D相碰经过的时间.
(1)设A、B碰撞后速度分别为v1、v2,根据动量守恒和机械能两守恒得:
mv0=mv1+1.5mv2
m1 2
=v 20
m1 2
+v 21
•1.5m1 2 v 22
联立解得:
v1=-
v0(负号表示A球逆时针返回),v2=1 5
v04 5
(2)由上面解答可知,BC首先要碰撞,设B和C相碰结合在一起后速度为v3,则由动量守恒有:
1.5mv2=3mv3
得:v3=
v2=1 2
v02 5
设管对球沿水平方向的压力N,此力提供D球做匀速圆周运动的向心力,根据牛顿第二定律得:
N=3m•
=v 23 R
,12m v 20 25R
由牛顿第三定律得知,B和C相碰结合在一起后对管沿水平方向的压力大小:
N′=N=
;12m v 20 25R
(3)A、B碰后,B经时间t1与C相碰,再经时间t2,D与A相碰
t1=
=2πR 3v2 5πR 6v0
从A和B第一次相碰后,到D与A相碰:
v3t2+|v1|•(t1+t2)=4πR 3
得:t2=35πR 18v0
∴A和B第一次相碰后,到A和D相碰经过的时间t为:
t=t1+t2=25πR 9v0
答:
(1)A和B第一次相碰后各自的速度大小分别为
v0和1 5
v0;4 5
(2)B和C相碰结合在一起后对管沿水平方向的压力大小为
;12m v 20 25R
(3)A和B第一次相碰后,到A和D相碰经过的时间为
.25πR 9v0