问题
问答题
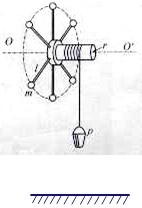
如图,在半径为r的轴上悬挂一个质量为M的水桶p,轴上分布着6根手柄,柄端有6个质量为m的金属小球.球离轴心的距离为l,轮轴、绳及手柄的质量以及摩擦均不计.开始时水桶p在离地面某高度处,释放后水桶p带动整个装置转动,当转动n周后,水桶恰好到达地面并停在地面不跳起,而绳继续释放.当绳释放完后,由于惯性,继续转动着的轮轴再次把绳绕在筒上,从而又把重物从地面提升起来.
求:(1)转动n周后水桶p的速率v;
(2)重物提升起的最大高度h.
答案
(1)设水桶p着地时的速度为v,小球转动的线速度为vˊ,
=v′ v
①L r
根据机械能守恒定律,有:
Mgn2πr=
Mv2+6×1 2
mv2②1 2
由①②得,
v=
③4nπMgr M+6m L2 r2
(2)水桶p着地后,由于惯性,轮轴继续转动,先把绳子放松,以后再次把绳绕在筒上,从而又把重物从地面提升起来.在这过程中,6个小球的动能全部转化为水桶p的重力势能.
6×
mv2=Mgh④1 2
由①①④得,
h=12πnmL2 r(M+6m
)L2 r2
答:
(1)转动n周后水桶p的速率v为
;4nπMgr M+6m L2 r2
(2)重物提升起的最大高度h为
.12πnmL2 r(M+6m
)L2 r2
