问题
问答题
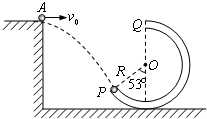
如图竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高.一质量m=0.8kg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上P点的切线方向进入轨道内侧,轨道半径OP与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0.6,g取10/m2.试求:
(1)小球从平台上的A点射出时的速度大小v0;
(2)小球从平台上的射出点A到圆轨道人射点P之间的距离l;(结果可用根式表示)
(3)小球沿轨道通过圆弧的最高点Q时对轨道的压力大小.
答案
(1)小球从A到P的高度差h=R(1+cos53°)①
小球做平抛运动有h=
gt2 ②1 2
则小球在P点的竖直分速度vy=gt③
把小球在P点的速度分解可得tan53°v0=vy④
由①②③④解得:小球平抛初速度v0=3m/s
(2)小球平抛下降高度h=
vyt1 2
水平射程s=v0t
故A、P间的距离
l=
=h2+s2
m2 13 5
(3)小球从A到达Q时,根据机械能守恒定律可知vQ=v0=3m/s
在Q点根据向心力公式得:
m
=N+mgvQ2 R
解得;N=m
-mg=14.4-8=6.4NvQ2 R
根据牛顿第三定律得:小球沿轨道通过圆弧的最高点Q时对轨道的压力N′=N=6.4N
答:(1)小球从平台上的A点射出时的速度大小为3m/s;
(2)小球从平台上的射出点A到圆轨道人射点P之间的距离
m;2 13 5
(3)小球沿轨道通过圆弧的最高点Q时对轨道的压力大小为6.4N
