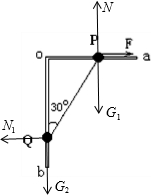
如图所示，光滑的直角细杆AOB固定在竖直平面内，OA杆水平，OB杆

问题问答题

如图所示，光滑的直角细杆AOB固定在竖直平面内，OA杆水平，OB杆竖直．有两个质量相等均为0.3kg的小球a与b分别穿在OA、OB杆上，两球用一轻绳连接，轻绳长L=25cm．两球在水平拉力F作用下目前处于静止状态，绳与OB杆的夹角θ=53°（sin37°=0.6，cos37°=0.8，sin53°=0.8，cos53°=0.6），求：

（1）此时细绳对小球b的拉力大小，水平拉力F的大小；

（2）现突然撤去拉力F，两球从静止开始运动，设OB杆足够长，运动过程中细绳始终绷紧，则当θ=37°时，小球b的速度大小．

答案

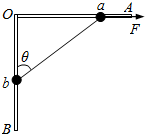
（1）以小球b为研究对象，设绳子拉力为T，由小球b受力平衡得：

Tcos53°=m_bg

则得 T=

mbg

cos53°

°=

0.3×10

0.6

N=5N

对小球a和小球b整体考虑，拉力F等于OB杆对b球的弹力

所以F=m_bgtan53°=0.3×10×

N=4N；

（2）对小球a和b整体用机械能守恒定律，有

m_bg（Lcos37°-Lcos53°）=

m_bv_b²+

m_av_a²

同时，小球a和b的速度满足

v_bcos37°=v_asin37°

两式联立，解得：v_b=0.6m/s；

答：

（1）此时细绳对小球b的拉力大小是5N，水平拉力F的大小是4N；

（2）现突然撤去拉力F，两球从静止开始运动，设OB杆足够长，运动过程中细绳始终绷紧，当θ=37°时，小球b的速度大小是0.6m/s．