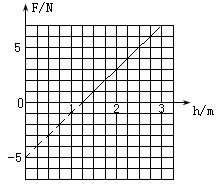
如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道和与之相切的圆形轨道连接而成，一小球从斜面轨道上静止开始下滑，然后沿圆形轨道运动。在圆形轨道的最高点放一个压力传感器，测得小球对轨道的压力，并通过计算机显示出来，当小球在斜面的下滑起始高度改变时，得到压力与下滑起始高度的图像如图，g取10 m/s2，不计空气阻力，求：
（1）小球的质量和圆形轨道的半径。
（2）试证明：小球运动到圆轨道的最低点与最高点时对轨道的压力差与小球的下滑高度无关。
（1）0.1kg 0.5m （2）见解析
（1）设小球在斜面的下滑起始高度为h，轨道半径为R，由机械能守恒定律；
mgh=2mgR+
(2分)
在最高点由牛顿第二定律得N+mg=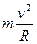
(2分)
由以上两式得N=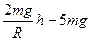
(2分)
由图象得：截距-5mg="-5 " 得质量m="0.1kg " (1分)
因为图线的斜率k=
得R="0.5m " (1分)
（2）证明：设小球运动到圆轨道的最低点和最高点的速度分别为v1和v2，对轨道的压力分别为N1、N2
最低点N1-mg=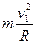
(1分)
最高点时N2+mg=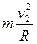
(1分)
在最高低到最高点的过程中由机械能守恒定律得
(2分)
由以上三式得N1-N2="6mg " (2分)
由结果可知，小球运动到圆轨道的最低点与最高点时对轨道的压力差与小球的下滑高度无关。 (1分)