问题
问答题
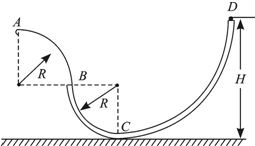
如图所示,由光滑细管组成的轨道固定在竖直平面内,其中AB段和BC段是半径为R的四分之一圆弧.一小球从距离水平地面高为H的管口D处静止释放,最后能够从A点水平抛出落到地面上.若R可以变化,求:
(1)R的最大值;
(2)小球从A点平抛落地时的水平位移x的最大值.
答案
(1)为使小球能够从A点平抛,需满足:mg+N=m v 2A R
且N≥0.
小球从D点静止释放运动到A点的过程中机械能守恒,故有:
mgH=mg•2R+
m1 2 v 2A
联立解得:R≤
H,所以R的最大值为2 5
H.2 5
(2)小球从A点平抛,根据平抛运动的规律有:
水平方向上:x=vAt
竖直方向上:2R=
gt21 2
联立解得:x=8R(H-2R)
显然,当R=
时,小球从A点平抛的水平位移有最大值 xmax=H.H 4
答:(1)R的最大值是
H;2 5
(2)小球从A点平抛落地时的水平位移x的最大值是H.
