问题
填空题
已知点P是半径为2的⊙O外一点,PA是⊙的切线,切点为A,且PA=2,在⊙O内作长为2
|
答案
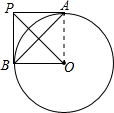
连接OA,
(1)如图,当弦AB与PA在O的同旁时,
∵PA=AO=2,PA是⊙的切线,
∴∠AOP=45°,
∵OA=OB,
∴∠BOP=∠AOP=45°,
而OP=OP,
∴△POA≌△POB,
∴PB=PA=2;
(2)如图,当弦AB与PA在O的两旁,连接OA,OB,
∵PA是⊙O的切线,
∴OA⊥PA,
而PA=AO=2,
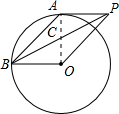
∴OP=2
;2
∵AB=2
,2
而OA=OB=2,
∴AO⊥BO,
∴PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=1,
∴BC=
,5
∴PB=2
.5
