问题
问答题
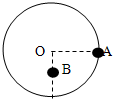
如图所示,半径为r,质量不计的圆盘盘面与地面相垂直,圆心处有一个垂直盘面的光滑水平固定轴O,在盘的最右边缘固定一个质量为m的小球A,在O点的正下方离O点
处固定一个质量也为m的小球B.放开盘让其自由转动,问:r 2
(1)当A球转到最低点时,两小球的重力势能之和减少了多少?
(2)A球转到最低点时的线速度是多少?
(3)在转动过程中半径OA向左偏离竖直方向的最大角度是多少?
答案
(1)当A球转到最低点时,A的重力势能减小mgr,B的重力势能增加mg
,所以两小球的重力势能之和减少为△EP=mgr-mgr 2
=r 2
mgr1 2
(2)取圆盘最低处的水平面势能为零,
由机械能守恒定律可得:mgr=mg
+r 2
m(ωr)2+1 2
m(ω×1 2
)2,r 2
又 vA=ωR,
解得vA=0.8gr
(3)设OA向左偏离竖直方向的最大角度是θ,
由系统机械能守恒定律得
mgr×cosθ-mg
×(1+sinθ)=0r 2
得 2cosθ=1+sinθ,
4(1-sin2θ)=1+2sinθ+sin2θ,
5sin2θ+2sinθ-3=0
sinθ=0.6
∴θ=37°
答:
(1)当A球转到最低点时,两小球的重力势能之和减少了
mgr.1 2
(2)A球转到最低点时的线速度是
.0.8gr
(3)在转动过程中半径OA向左偏离竖直方向的最大角度是37°.

