问题
解答题
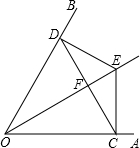
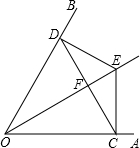
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
(1)求证:∠ECD=∠EDC;
(2)若∠AOB=60°,OE=8,试求EF的长.
答案
(1)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=ED.
∴△EDC为等腰三角形.
∴∠ECD=∠EDC.
(2)∵在Rt△DEO和Rt△CEO中,
∵EO=EO,DE=EC(已证),
∴Rt△DEO≌Rt△CEO(HL),
∴DO=CO,
∵∠AOB=60°,OE是∠AOB的平分线,
∴∠EOC=30°,△DOC是等边三角形,
∴∠OCD=60°,
∵EC⊥OA,
∴∠ECO=90°.
∴∠ECF=30°,
∴EC=
OE=4,1 2
∴EF=
EC=1 2
×4=2.1 2