问题
问答题
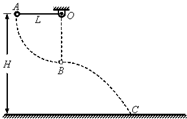
如图所示,质量m=2kg的小球用长L=1.05m的轻质细绳悬挂在距水平地面高H=6.05m的O点.现将细绳拉直至水平状态自A点无初速度释放小球,运动至悬点O的正下方B点时细绳恰好断裂,接着小球作平抛运动,落至水平地面上C点.不计空气阻力,重力加速度g取10m/s2.求:
(1)细绳能承受的最大拉力;
(2)细绳断裂后小球在空中运动所用的时间;
(3)小球落地瞬间速度的大小;
(4)现换用同样的轻质细绳,仅使绳长变为L1,其他条件不变,重复上述过程.当L1为何值时,小球落地点距B点的水平距离最大?
答案
(1)小球从A→B过程,根据机械能守恒定律得:mgL=
m1 2
-0v 2B
经B点时,由牛顿第二定律得:FB-mg=m v 2B L
解得:最大拉力FB=3mg=3×2×10N=60N
(2)小球从B→C过程做平抛运动,则有:H-L=
gt21 2
解得:t=
=2(H-L) g
s=1s 2×(6.05-1.05) 10
(3)从A→B→C过程,根据机械能守恒得:mgH=
m1 2
-0v 2C
解得:vC=
=2gH
m/s=11m/s 2×10×6.05
(4)从A1→B1过程,根据机械能守恒得:mgL1=
mv2-01 2
B1→C1过程:H-L1=
gt1 2 21
x1=vt1
联立得:x1=4L1(H-L1)
当L1=H-L1,即L1=
=H 2
m=3.025m时,水平距离x1最大.6.05 2
答:(1)细绳能承受的最大拉力为60N;(2)细绳断裂后小球在空中运动所用的时间为1s;(3)小球落地瞬间速度的大小为11m/s;(4)当L1为3.025m时,小球落地点距B点的水平距离最大.
