问题
问答题
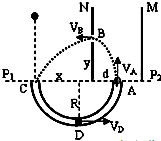
如图所示,p1,p2为一水平面,其上方紧贴放置一对竖直正对的带电金属板M、N,其下方紧贴放置一内壁光滑的绝缘轨道ADC,绝缘轨道ADC位于竖直平面内,右端A恰在两板的正中央处,N板上开有小孔B,孔B到水面P1,P2的距离为绝缘轨道直径的
倍.设仅在M、N两板之间存在匀强电场.现在左端C的正上方某一位置,将一质量为m、电荷量为q的小球静止释放,经过绝缘轨道CDA后从A端竖直向上射入两板间,小球能从B孔水平射出,并恰好落到c端.整个过程中,小球的电荷量不变,孔B的大小及小球的直径均可忽略,重力加速度为g.求:2 3
(1)板间电场强度E;
(2)小球运动到绝缘轨道最低点D时对轨道的压力大小.
答案
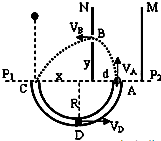
(1)如图,设绝缘轨道半径为R,A到板N距离为d,AB的竖直距离为y,C到板N的距离为x;到达最低点D的速度为vD,到A点的速度为vA,到达孔B时的速度为vB.
球在离开A经B到C的过程中,竖直方向小球受重力作用,故从A到B和从B到C的时间相等,并设从A到B的时间为t.
则有:d=
tvB 2
x=vBt
联立解得:x=2d
由题意可得,y=
(x+d)2 3
在水平方向上,有d=1 2
t2Eq m
在竖直方向上,有:y=
gt21 2
解得板间场强大小为:E=
;mg 2q
(2)从A到B的过程中,有vA2=2gy
由题意可得x+d=2R
联立解得vA2=
Rg8 3
从D到A,根据机械能守恒,有
mvD2=mgR+1 2
mvA21 2
在D点,有:F-mg=mv 2D R
解得F=
mg;17 3
答:(1)板间场强为
;(2)小球运动到绝缘轨道最低点D时对轨道的压力为mg 2q
mg.17 3