问题
解答题
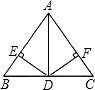
如图，在△ABC中，∠B=∠C，D是BC的中点，且DE⊥AB，DF⊥AC，E，F为垂足，求证：AD平分∠BAC．
答案
证明：∵D是BC的中点，
∴BD=CD，
又∵DE⊥AB，DF⊥AC，
∴∠BED=∠CFD=90°，
在△BED和△CFD中，
，∠BED=∠DFC ∠B=∠C BD=CD
∴△BED≌△CFD中（AAS），
∴ED=FD．
又∵DE⊥AB，DF⊥AC，
∴AD平分∠BAC．
搜题请搜索小程序“爱下问搜题”