问题
选择题
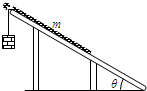
如图所示,倾角θ=30°的粗糙斜面固定在地面上,长为l、质量为m、粗细均匀、质量分布均匀的软绳置于斜面上,其上端与斜面顶端平齐.用细线将质量为3m物块与软绳连接,物块由静止释放后向下运动,直到软绳刚好全部离开斜面(此时物块未到达地面),若软绳与斜面之间动摩擦因数为常数μ=
,且软绳在斜面上任意位置时,支持力均匀作用在软绳底部,则在此过程中下列说法正确的是( )3 6
A.物块的机械能逐渐增加
B.软绳全部刚离开斜面时的速度为5 4 gl
C.软绳克服摩擦力所做的功为
mgl1 4
D.软绳的动能增量与克服摩擦力所做的功之和为3mgl
答案
A、物块下落过程中,软绳对物块做负功,物块的机械能逐渐减小,A错误;
B、对系统应用能量守恒:3mgL+mg×
(1-sinθ)=L 2
(3m+m)v2+1 2
μmgcosθ,解得:v=L 2 5 4
,B正确;gl
C、软绳克服摩擦力所做的功为
μmgcos30°=L 2
mg.故C错误;L 8
D、软绳的动能增量与克服摩擦力所做的功之和为重力势能的减少量:3mgL+
mg(1-sin30°)=L 2
mgL.故D错误.13 4
故选:B.
