问题
问答题
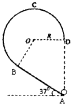
如图,在竖直平面内有一固定光滑轨道,其中AB部分是倾角为37°的直轨道,BCD部分是以O为圆心、半径为R的圆弧轨道,两轨道相切于B点,D点与O点等高,A点在D点的正下方.质量为m的小球在沿斜面向上的拉力F作用下,从A点由静止开始做变加速直线运动,到达B点时撤去外力.已知小球刚好能沿圆轨道经过最高点C,然后经过D点落回到A点.已知sin37°=0.6,cos37°=0.8,重力加速度大小为g.求
(1)小球在C点的速度的大小;
(2)小球在AB段运动过程,拉力F所做的功;
(3)小球从D点运动到A点所用的时间.
答案
(1)在C点:由牛顿第二定律得,mg=mv 2C R
解得:vC=gR
(2)已知θ=37°外力在AB段所做的功为W,由几何关系得:AB=
=2RR+Rsinθ cosθ
从B到C,根据机械能守恒定律
m1 2
=v 2B
m1 2
+mg(R+Rcosθ)v 2C
从A到B,根据动能定理,
W-mg2Rsinθ=
m1 2 v 2B
联立解得:W=
mg7 2
(3)从C到D,根据机械能守恒定律,
m1 2
=v 2D
m1 2
+mgRv 2C
解得:vD=3gR
从C到A,根据机械能守恒定律,
mv1 2
=2A
m1 2
+mg3Rv 2C
解得:vA=7gR
从D到A做匀加速直线运动,根据运动学公式,
AD=
(vD+vA)t1 2
解得:t=(
-7
)3 R g
答:
(1)小球在C点的速度的大小为
;gR
(2)小球在AB段运动过程,拉力F所做的功为
mg;7 2
(3)小球从D点运动到A点所用的时间为(
-7
)3
.R g
