问题
问答题
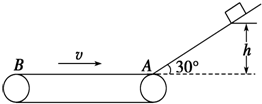
如图所示,倾角为30°的光滑斜面的下端有一水平传送带,传送带正以6m/s的速度运动,运动方向如图所示.一个质量为2kg的物体(物体可以视为质点),从h=3.2m高处由静止沿斜面下滑,物体经过A点时,不管是从斜面到传送带还是从传送带到斜面,都不计其动能损失.物体与传送带间的动摩擦因数为0.5,g=10m/s2,则:
(1)物体由静止沿斜面下滑到斜面末端的速度大小?
(2)为使物体不掉下传送带,传送带左右两端AB间的距离L至少为多少?
(3)物体在传送带上先向左运动后向右运动,最后沿斜面上滑所能达到的最大高度h′为多少?
答案
(1)物体由光滑斜面下滑的过程,只有重力做功,机械能守恒,则得:
mgh=
mv21 2
解得:v=
=2gh
m/s=8m/s2×10×3.2
(2)当物体滑到传送带最左端速度为零时,AB间的距离L最小,由动能定理得:
-μmgL=0-
mv21 2
解得:L=
=v2 2μg
m=6.4m82 2×0.5×10
(3)物体在到达A点前速度与传送带相等,最后以v带=6m/s的速度冲上斜面,则根据动能定理得:
由0-
mv带2=0-mgh′1 2
得:h′=
=v 2带 2g
m=1.8m.62 2×10
答:
(1)物体由静止沿斜面下滑到斜面末端的速度大小为8m/s.
(2)为使物体不掉下传送带,传送带左右两端AB间的距离L至少为6.4m.
(3)物体在传送带上先向左运动后向右运动,最后沿斜面上滑所能达到的最大高度h′为1.8m.
