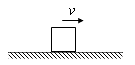
如图所示,半径R=0.8m的光滑
圆弧轨道固定在水平地面上,O为该圆弧的圆心,轨道上方的A处有一个可视为质点的质量m=1kg的小物块,小物块由静止开始下落后恰好沿切线进入1 4
圆弧轨道.此后小物块将沿圆弧轨道下滑,已知AO连线与水平方向的夹角θ=45°,在轨道末端C点紧靠一质量M=3kg的长木板,木板上表面与圆弧轨道末端的切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,g取10m/s2.求:1 4
(1)小物块刚到达C点时的速度大小;
(2)小物块刚要到达圆弧轨道末端C点时对轨道的压力;
(3)要使小物块不滑出长木板,木板长度L至少为多少?
(1)小物块从A到C,根据机械能守恒有:
mg•2R=
mv1 2
,2C
解得:vC=
=4gR
m/s=44×10×0.8
m/s.2
(2)小物块刚要到C点,由牛顿第二定律有:
FN-mg=
,m v 2C R
解得:FN=mg+
=1×10+m v 2C R
N=50N.1×(4
)22 0.8
由牛顿第三定律,小物块对C点的压力FN′=50N,方向竖直向下.
(3)设小物块刚滑到木板右端时达到共同速度,大小为v,小物块在长木板上滑行过程中,小物块与长木板的加速度分别为
am=μmg m
aM=μmg M
由运动学公式得:v=vC-amt,v=aMt
由能量守恒定律得:-μmgL=
(M+m)v2-1 2
mv1 2 2C
联立解得:L=4m.
答:(1)小物块刚到达C点时的速度大小为4
m/s;2
(2)小物块刚要到达圆弧轨道末端C点时对轨道的压力为50N;
(3)要使小物块不滑出长木板,木板长度L至少为4m.