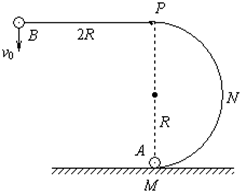
如图所示,光滑半圆形轨道MNP竖直固定在水平面上,直径MP垂直于水平面,轨道半径R=0.5m.质量为m1的小球A静止于轨道最低点M,质量为m2的小球B用长度为2R的细线悬挂于轨道最高点P.现将小球B向左拉起,使细线水平,以竖直向下的速度v0=4m/s释放小球B,小球B与小球A碰后粘在一起恰能沿半圆形轨道运动到P点.两球可视为质点,g=10m/s2.试求
①B球与A球相碰前的速度大小;
②A、B两球的质量之比m1:m2.
①B球下摆过程中机械能守恒,
由机械能守恒定律得:
m2v02+m2g•2R=1 2
m2v12,1 2
解得:v1=6m/s;
②两球恰好到达P点,由牛顿第二定律得:
(m1+m2)g=(m1+m2)
,解得:vP=v 2P R
m/s,5
两球从M到P过程中,由动能定理得:
(m1+m2)vP2-1 2
(m1+m2)v22=-(m1+m2)g•2R,1 2
解得:v2=5m/s;
两球碰撞过程动量守恒,以两球组成的系统为研究对象,
以B球的初速度方向为正方向,由动量守恒定律得:
m2v1=(m1+m2)v2,解得:
=m1 m2
;1 5
答:①B球与A球相碰前的速度大小为6m/s;
②A、B两球的质量之比m1:m2=1:5.
