问题
问答题
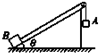
质量均为m的小物体A和B分别系在一根不计质量的细绳两端,绳子跨过固定在倾角θ=30°的斜面顶端的定滑轮上,且斜面固定在水平地面上.开始时把物体B拉到斜面底端,绳与斜面平行,这时物体A离地面的高度为1.8m,如图所示,若不计一切摩擦,从静止开始放手让它们运动,g取10m/s2,求:
(1)物体A着地时的速度;
(2)物体A着地后(即静止于地面)物体B沿斜面上滑的最大距离.(设斜面足够长)
答案
(1)设A落地时的速度为v,AB组成的系统机械能守恒,则得:
mgh-mghsinθ=
•2mv2,1 2
代入数据得:v=
=
gh1 2
m/s=3m/s.
×10×1.81 2
(2)A落地后,B以v为初速度沿斜面匀减速上升,设沿斜面又上升的距离为S,
由动能定理得:-mgssinθ=0-
mv2 1 2
代入数据得:s=
=v2 g
m=0.9m.32 10
答:
(1)物体A着地时的速度为3m/s;
(2)物体A着地后(即静止于地面)物体B沿斜面上滑的最大距离为0.9m.
