问题
问答题
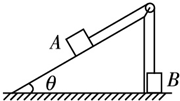
如图,一固定的斜面,其倾角为θ=30°,另一边与水平地面垂直,顶端有一定滑轮,跨过定滑轮的细线两端分别与物块A、B相连,A的质量为4m,B的质量为m.开始时,将B按在地上不动,然后放手,让A沿斜面下滑而B上升,所有摩擦均忽略不计.当A下滑距离为S时,细线突然断了.求B上升的最大高度.(设B不会与定滑轮相碰)
答案
设细线断前一瞬间A和B速度的大小为v,A沿斜面下滑S的过程中,A的高度降低了Ssinθ,B的高度升高了S,物块A和B以及地球组成的系统机械能守恒,物块A机械能的减少量等于物块B机械能的增加量,即:
4mgSsinθ-
•4mv2=mgS+1 2
mv21 2
细线断后,物块B做竖直上抛运动,物块B与地球组成的系统机械能守恒,设物块B继续上升的高度为h,有:
mgh=
mv21 2
联立两式得:h=
,故物块B上升的最大高度为:H=S+h=S+S 5
=S 5
S,6 5
答:B上升的最大高度为
S.6 5
