问题
问答题
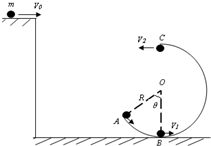
如图所示,质量m=2kg的小球以初速度V0沿光滑的水平面飞出后,恰好无碰撞地进入光滑的圆弧轨道,其中圆弧AB对应的圆心角θ=530,圆半径R=0.5m.若小球离开桌面运动到A点所用时间t=0.4s.(sin53°=0.8cos53°=0.6g=10m/s2)
(1)求小球沿水平面飞出的初速度V0的大小?
(2)到达B点时,求小球此时对圆弧的压力N1大小?
(3)小球是否能从最高点C飞出圆弧轨道,并说明原因.
答案
(1)小球开始做平抛运动,有:vy=gt
根据几何关系,有:tanθ=vy v0
代入数据,解得:v0=3m/s
(2)小球在A点的速度:vA=vy sinθ
小球从点A运动到点B时,满足机械能守恒定律,有:
m1 2
+mgR(1-cosθ)=v 2A
m1 2 v 21
小球运动到点B时,根据受力情况有:N-mg=mv 21 R
代入数据,解得:N=136N
小球此时对圆弧的压力:N′=N=136N
(3)小球从点B运动到点C时,满足机械能守恒定律,有:
m1 2
+mg•2R=v 21
m1 2 v 22
又:F向=mv 22 R
代入数据,解得:F向=36N>mg
所以小球能从C点飞出.
答:(1)求小球沿水平面飞出的初速度V0的大小为3m/s;
(2)到达B点时,求小球此时对圆弧的压力N1大小为136N;
(3)小球能从最高点C飞出圆弧轨道.
