问题
问答题
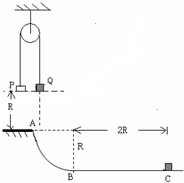
如图所示,在平台右侧紧靠着用同种材料制成的轨道ABC,AB段为四分之一圆弧,半径为R=1m,水平放置的BC段足够长.现有两个质量分别为3kg和1kg的物块P和Q,用一段质量不计的细绳挂在光滑的定滑轮的两端,先用手托着P,使两物块等高且距离平台也为R,物块与BC轨道的动摩擦因数为μ=0.1,现释放物块P,在P物块刚落地时剪断细线,之后Q会恰好落入ABC轨道继续滑行,且停在C点,BC=2R,求:
(1)P物块落地时P和Q共同的速度多大
(2)物块在AB段克服摩擦力做功多少.
答案
(1)P物块下落过程,对于PQ组成的系统,在P落地前只有重力做功,系统的机械能守恒,则有:
mPgR-mQgR=
(mP+mQ)v21 2
得:v=
=2(mP-mQ)gR mP+mQ
m/s=2×(3-1)×10×1 3+1
m/s10
(2)对于Q物块,根据动能定理得:mQg•3R-W-μmQg•R=0-
mQv21 2
解得:物块Q在AB段克服摩擦力做功为:
W=mQg•3R-μmQg•R+
mQv2=3×10×3-0.1×3×10×1+1 2
×3×(1 2
)2=102J10
答:(1)P物块落地时P和Q共同的速度为
m/s.10
(2)物块在AB段克服摩擦力做功102J.
