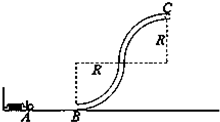
某同学玩“弹珠游戏”装置如图所示,S形管道BC由两个半径为R的
圆形管道拼接而成,管道内直径略大于小球直径,且远小于R,忽略一切摩擦,用质量为m的小球将弹簧压缩到A位置,由静止释放,小球到达管道最高点C时对管道恰好无作用力,求:1 4
(1)小球到达最高点C的速度大小;
(2)若改用同样大小质量为2m的小球做游戏,其它条件不变,求小球能到达的最大高度;
(3)若改用同样大小质量为
的小球做游戏,其它条件不变,求小球落地点到B点的距离.m 4
(1)由于小球到达管道最高点C时对管道恰好无作用力,根据牛顿第二定律和向心力公式有:mg=m
,v 2C R
解得小球到达最高点C的速度大小为:vC=gR
(2)由于忽略一切摩擦,因此小球与弹簧组成的系统机械能守恒,因此根据机械能守恒定律可知,弹簧弹性势能为:Ep=
mv1 2
+2mgR=2C
mgR5 2
改用质量为2m的小球时,因为Ep=
mgR<4mgR,所以小球不能到达C点,设此时小球能到达的最大高度为h,根据机械能守恒定律有:5 2
Ep=2mgh,
解得:h=
R5 4
(3)改用质量为
的小球时,小球能通过最高点C后做平抛运动,设此时离开C点的速度为v,根据机械能守恒定律有:m 4
Ep=
•1 2
v+m 4
mgR1 2
根据平抛运动的规律可知,此时小球离开C点后做平抛运动的水平射程:x=v4R g
联立以上各式解得:x=8R
根据图中几何关系可知,小球落地点到B点的距离为:d=x+2R=10R
答:(1)小球到达最高点C的速度大小为
;gR
(2)小球能到达的最大高度为
R;5 4
(3)小球落地点到B点的距离为10R.
