问题
问答题
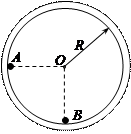
如图所示的半径为R的光滑圆形轨道固定在竖直面内，质量为m的小球A以竖直向下的速度v从与圆心等高处开始沿轨道向下运动，与静止于轨道最低点的B球相撞，碰撞后A、B球恰能分别到达左右两边与圆心等高处。已知地球表面的重力加速度为g。试求：
（1）小球B的质量M＝？
（2）第一次碰撞刚结束时小球A对轨道的压力大小？
答案
(1)（1+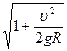
）m (2) 3 mg
设小球A在与B球相撞前的速度大小为v1，根据机械能守恒
mgR +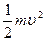
＝
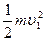············（4分）
得v1＝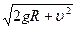
·····（2分）
由于碰撞后A、B球都恰能达到与圆心等高处，所以第一次碰撞刚结束时小球A、B的速度大小相等，方向相反，设速度大小为v2，根据机械能守恒
v2＝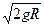
········（4分）
设小球B的质量为M，根据动量守恒
mv1＝Mv2－mv2···········（4分）
解得M＝（1+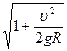）m········（2分）
（2）设第一次碰撞结束时小球A对轨道的压力大小为N，轨道对小球A的支持力为N′，则FN＝FN′···························································（2分）
根据牛顿第二定律FN′－mg＝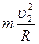
·······（2分）
解得FN＝FN′＝3 mg· ····（2分）