问题
解答题
过点P（2，1）作抛物线y2=4x的弦AB，若弦恰被P点平分，
（1）求直线AB所在直线方程；（用一般式表示）
（2）求弦长|AB|。
答案
解：（1）设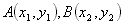
，
则
，
由于直线的斜率存在，故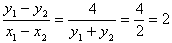
，
从而直线AB的方程为：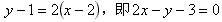
；
（2）
，
因△＞0，故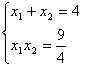
，
于是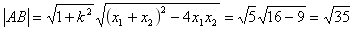
。
搜题请搜索小程序“爱下问搜题”
过点P（2，1）作抛物线y2=4x的弦AB，若弦恰被P点平分，
（1）求直线AB所在直线方程；（用一般式表示）
（2）求弦长|AB|。
解：（1）设，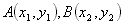
则，
由于直线的斜率存在，故，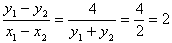
从而直线AB的方程为：；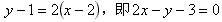
（2），
因△＞0，故，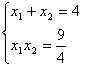
于是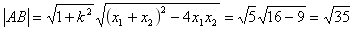。