问题
计算题
（14分）如图所示，半径R=0．8 m的四分之一光滑圆弧轨道竖直固定，轨道末端水平，其右方有横截面半径r=0．2 m的转筒，转筒顶端与轨道最低点B等高，下部有一小孔，距顶端h=0．8m，转筒的轴线与圆弧轨道在同一竖直平面内，开始时小孔也在这一平面内的图示位置。现使一质量m=0．1kg的小物块自最高点A由静止开始沿圆弧轨道滑下，到达轨道最低点B时转筒立刻以某一角速度匀速转动起来，且小物块最终正好进入小孔。不计空气阻力，g取l0m/s2，求：
（1）小物块到达B点时对轨道的压力大小；
（2）转筒轴线距B点的距离L；
（3）转筒转动的角速度ω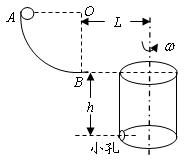
答案
（1）F/N=3N
（2）1．8m
（3）
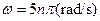（n=1,2,3……）
（1）从A到B，只有重力做功，根据机械能守恒定律，得
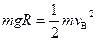（2分）
在B点，根据牛顿第二定律有
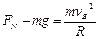（2分）
代入数据解得FN="3N " （1分）
根据牛顿第三定律可知小物块到达B点时对轨道的压力为F/N="3N " （1分）
（2）滑块从B点开始做平抛运动，设滑块从B点到进入小孔的时间为t
，
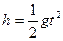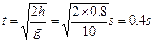（2分）
L=r+vBt=（0．2+4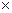
0．4）m=1．8m （2分）
（3）在小球平抛的时间内，圆桶必须恰好转整数转，小球才能钻入小孔
即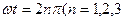
……）（2分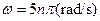）（n=1,2,3……） （2分）