问题
计算题
（10分）如图所示，竖直平面内的光滑弧形轨道的底端恰好与光滑水平面相切。质量为M=2.0kg的小物块B静止在水平面上。质量为m=1.0kg的小物块A从距离水平面高h＝0.45m的P点沿轨道从静止开始下滑，经过弧形轨道的最低点Q滑上水平面与B相碰，碰后两个物体以共同速度运动。取重力加速度g=10m/s2。求
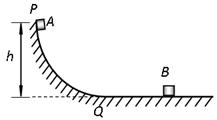
（1）A经过Q点时速度的大小v0；
（2）碰撞过程中系统（A、B）损失的机械能ΔE.
答案
（1）3.0m/s
（2）3.0J
（1）A从P滑到Q的过程中，根据机械能守恒定律得
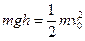（ 2分）
解得A经过Q点时速度的大小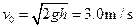
（2分）
（2）A与B相碰，根据动量守恒定律得
mv0=(m + M ) v （1分）
解得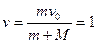 
.0m/s （2分）
根据能量守恒定律得
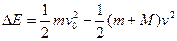（2分）
解得A与B碰撞过程中系统损失的机械能ΔE = 3.0 J （ 1分）