问题
计算题
如图所示，皮带在轮O1O2带动下以速度v匀速转动，皮带与轮之间不打滑。皮带AB段长为L，皮带轮左端B处有一光滑小圆弧与一光滑斜面相连接。物体无初速放上皮带右端后，能在皮带带动下向左运动，并滑上斜面。己知物体与皮带间的动摩擦因数为μ，且
求：（1）若物体无初速放上皮带的右端A处，则其运动到左端B处的时间。
（2）物体无初速的放上皮带的不同位置，则其沿斜面上升的最大高度也不同。设物体放上皮带时离左端B的距离为x，请写出物体沿斜面上升最大高度h与x之间的关系，并画出h-x图象。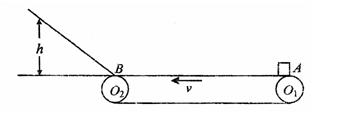
答案
解：（1）（7分）物体放上皮带运动的加速度α=μg （1分）
物体加速到v前进的位移x0=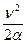
=
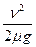（2分）
∵L＞x0, ∴物体先加速后匀速，加速时间t1=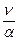
=
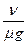（1分）
匀速时间t2=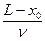
=
-
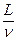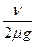（1分）
∴物体从A到B时间t= t1+t2=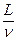+ 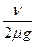（2分）
（2）（7分）当x≤x0时，物体一直加速，到B的速度为v1，则v21=2μgx
又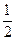
mv21="mgh " ∴h=
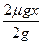=μx （3分）
当x＞x0时，物体先加速后匀速，到达B时速度均为v
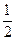mv2=" mgh " h′=
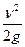（2分）
