问题
计算题
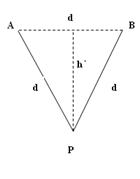
今年春天,我国西南地区遭遇百年不遇的特大干旱,在抗旱救灾的队伍中,我们的子弟兵战士翻山越岭为广大灾区人民送去“生命之水”,军民一心同自然灾害进行斗争。战士们通过山谷的一种方法可以简化为下面的情境:将一根长为2d、不可伸长的细绳两端固定在相距为d的A、B两等高点,绳上挂一小滑轮P,战士们相互配合,沿着绳子滑到对面,如图所示。战士甲用力拉住滑轮,质量为m的战士乙吊在滑轮上,脚离地,处于静止状态,此时AP竖直。然后战士甲将滑轮从静止释放。不计绳与滑轮的质量,忽略一切摩擦及空气阻力的影响,求:战士乙滑动过程中的最大速度Vm 。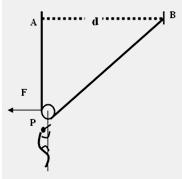
答案
乙在静止时由图中几何关系可知 h2+d2 = (2d-h)2,
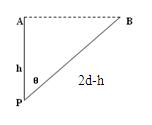
解得h= (3分)
(3分)
乙在滑动过程中机械能守恒,滑到绳子中点时位置最低,速度最快,此时A、P、B三点构成等边三角形,如图所示,P到AB的距离为h`=dcos300=
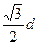 (3分)
(3分)
由机械能守恒,有mg(h`-h) =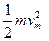 (5分)
(5分)
解得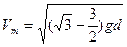 (4分)
(4分)