问题
计算题
如图所示，传送带以v为l0m／s速度向左匀速运行，BC段长L为2m，半径R为1.8m的光滑圆弧槽在B点与水平传送带相切．质量m为0.2kg的小滑块与传送带间的动摩擦因数为0.5，g取l0m／s2，不计小滑块通过连接处的能量损失．求：
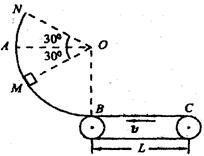
(1) 小滑块从M处无初速度滑下，到达底端B时的速度；
(2) 小滑块从M处无初速度滑下后，在传送带上向右运动的最大距离及此过程产生的
热量；
(3) 将小滑块无初速度放在传送带C端，要使小滑块能通过N点，传送带BC段至少为多长?
答案
解：（1）由机械能守恒定律可知：mgR(1-cos600)=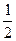
m
得vB=3
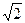m/s
（2）小滑块做匀减速运动至停止时距离最大
0-="-2aS " a="µg=5m/s2 " S="1.8m " t=
=
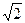s
Sm=vt+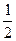vBt="10.2m " Q=fSm=10.2J
（3）小滑块能通过N点临界条件：m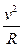
="mgsin300 " V=3m/s
由机械能守恒定律： -mgR(1+sin300)= 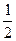mv2-m v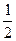B=
m/s
小滑块在传送带上加速过程：="2aS " S=6.3m