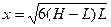问题
计算题
如图所示，一根不可伸长的轻绳两端各系一个小球a和
b，跨在两根固定在离地高度为H的光滑水平细杆A、B上，质量为m的b球与B的距离为L，质量为4m的a球放置于地面上。把b球从水平位置由静止释放，求：
（1）a球
对地面的最小压力
为多大？
（2）已知细线能承受的最大拉力Fm=4mg，现给b球竖直向下的初速度，当b球运动到B点的正下方时细线恰被拉断，求b球落地点与B点的水平距离。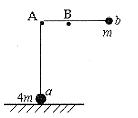
答案
（1）B球下落时，由机械能守恒有
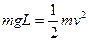（2分）
在最低点，设绳的拉力为FT，由牛顿第二定律有
（
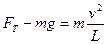2分）
设地面对a球的支持力为FN，由平衡条件有
FN+FT="4mg " （1分）
解得Ft=3mg，FN=mg。
由牛顿第三定律可知a球对地面的最小压力为mg。 （1分）
（2）b球运动到B点正下方时
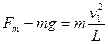（2分）
线断后b球做平抛运动，设所求水平距离为x
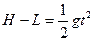（1分）
x=v1t （1分）
解得